Determinants of Resistance to Flow (Poiseuille's Equation)

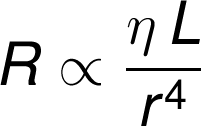Vessel resistance (R) is directly proportional to the length (L) of the vessel and the viscosity (η) of the blood, and inversely proportional to the radius to the fourth power (r⁴) or diameter to the fourth power (D⁴). Diameter can be substituted for radius because diameter and radius are directly proportionate to each other (D = 2r; therefore D ∝ r).

This relationship shows that a vessel having twice the length of another vessel (and each having the same diameter) will have twice the resistance to flow. Similarly, if the viscosity of the blood increases 2-fold, the resistance to flow will increase 2-fold. In contrast, an increase in diameter (or radius) reduces resistance. The change in diameter alters resistance to the fourth power of the change in diameter. For example, a 2-fold increase in diameter decreases resistance by 16-fold! Therefore, vessel resistance is exquisitely sensitive to changes in diameter.

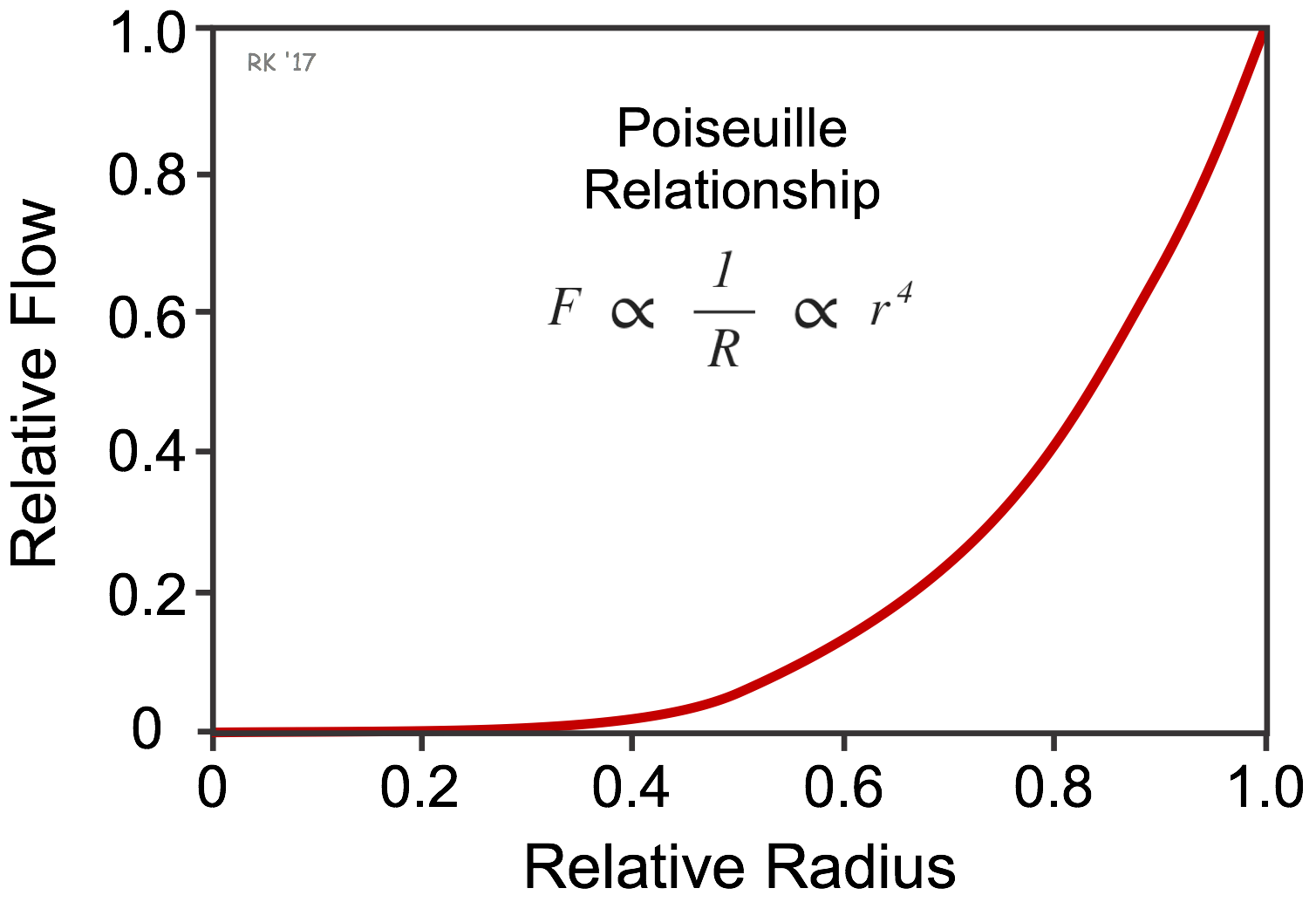The relationship between flow and vessel diameter to the fourth power (assuming constant ΔP, L, η and laminar flow conditions) is illustrated in the figure to the right. This figure shows how small decreases in radius dramatically reduce flow.

Vessel length does not change appreciably in vivo and, therefore, can be considered constant. Blood viscosity normally does not change very much; however, it can be significantly altered by changes in hematocrit, temperature, and by low flow states.

If the above expression for resistance is combined with the equation describing the relationship between flow, pressure, and resistance (F=ΔP/R), then

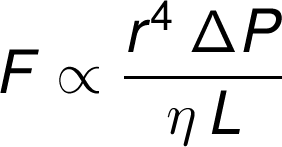
This relationship (based on Poiseuille's equation) was first described by the 19th century French physician Poiseuille. It describes how flow is related to perfusion pressure, radius, length, and viscosity. The full equation contains a constant of integration and pi, which are not included in the above proportionality.

In the body, however, flow does not conform exactly to this relationship because this relationship assumes long, straight tubes (blood vessels), a Newtonian fluid (blood, unlike water, is non-Newtonian), and steady, laminar flow conditions. The relationship, however, clearly shows the dominant influence of vessel diameter on resistance and flow. The relationship between diameter and resistance helps us to understand how physiological (e.g., vascular tone) and pathological (e.g., vascular stenosis) changes in vessel diameter alter pressure and flow.

The factors that determine resistance across a heart valve are the same as described above, except that length becomes insignificant because the path of blood flow across a valve is extremely short compared to a blood vessel. Therefore, when resistance to flow is described for heart valves, the primary factors considered are the cross-sectional area of the valve opening and blood viscosity. These hemodynamic principles are important to understand how changes in heart valve orifice size (e.g., in valvular stenosis) impact flow and pressure gradients across heart valves.

Revised 11/05/2023